| Logic Games Online | Play 5x5 Nurikabe | Daily 9x9 Nurikabe |
Nurikabe (sometimes called Islands in the Stream) is a binary determination puzzle. You must decide for each cell if it is white or black according to the following rules:
When played on paper, white cells are marked with a dot in the center and black cells are filled in. When playing nurikabe at Logic Games Online, unnumbered cells start out gray and cycle through white and black when clicked.
Play our daily 9x9 nurikabe or all the 5x5 nurikabe you can handle or read on for some tips on solving these puzzles.
Most nurikabe boards can be solved using logic to deduce which cells should be white and which ones black.
An island is full if it contains as many white cells as the number in the region. Any 1s are trivially full regions. When you encounter a full region, any cells that boarder it must be black. Here we show the cells that must be black due to a single celled white island.
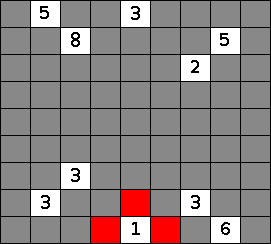
Since two numbers in a nurikabe puzzle cannot be part of the same island, any cell that has two numbered neighbors must be black. The two cases are when a cell is between two numbered cells, or (as in the image) when two numbered cells in the nurikabe are adjacent diagonally (second image).
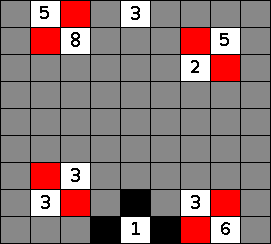
If an island in the nurikabe doesn't yet have its target number of cells, and there is only one cell bordering it that is not the opposite color, that cell must be part of the region. Note that this applies to black regions within the nurikabe, too, and to white regions that don't yet have a number. Here we show in red black cells into which black regions of the nurikabe must expand, and in green cells into which white regions must expand. The second image shows the result of applying this step a few more times and then putting black around the border cells of the two complete islands.
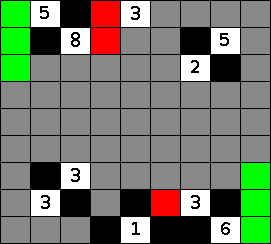

If a region of the nurikabe puzzle only needs one more cell and all the cells it could expand to border on one specific cell, then that cell must be black. No matter which cell the region expands into, this threatened cell will border the full region. This most commonly happens when there is a 2 with black cells or edges on two of its 4 sides. At this point in the nurikabe, this situation occurs in two different places. The possible completions of the two islands are shown in a blue-gray and the threatened cells in red.
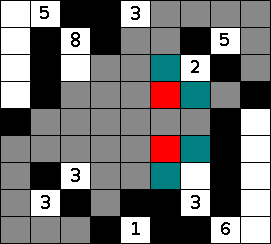
If no white islands in the nurikabe puzzle can expand far enough to reach a cell, then that cell must be black. This is easiest to evaluate on a cell by cell basis, looking for a cell in the nurikabe that seems far away from all islands. In this image, we have colored all the cells that each of the islands in the nurikabe can reach. Note that just one cell of the nurikabe is still gray, and therefore unreachable.
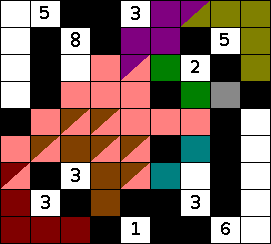
If there are three black cells in an L shape in the nurikabe puzzle, then the cell on the inside of the elbow must be white to avoid having a 2x2 square of black cells. Here we have one such elbow.

At times, it is obvious that coloring a cell in the nurikabe puzzle white or black simply won't work. In this case, it must be the opposite color. Here, the top right corner can't be black, as both the black region and the white region of the nurikabe would need to expand into the same cell.

Sometimes expanding a white or black region of the nurikabe in a certain direction wouldn't leave enough room for a neighboring region to grow, so a different direction must be chosen. Here we can see that the black region must escape through the red cell to connect to the rest of the black. Then it must go down, as cutting across to the left wouldn't leave enough room for the white region of the nurikabe with the 3 in it.

The techniques above should be enough to complete most nurikabe puzzles. If you do get to the point where you can't figure out any more cells, you can always guess at a cell and then work things out. Or, you can guess at the shape of a particular region in the nurikabe. Either way, try to pick a cell or region that will force he shapes of other regions, or the colors of other cells in the nurikabe.